Home Donate New Search Gallery Reviews How-To Books Links Workshops About Contact
|
I personally buy from Adorama, Amazon, Ritz, B&H, Calumet and J&R. I can't vouch for ads below.
|
Angle of View
© 2007 KenRockwell.com
I get my goodies at Ritz, Amazon and Adorama. It helps me keep adding to this site when you get yours from those links, too.
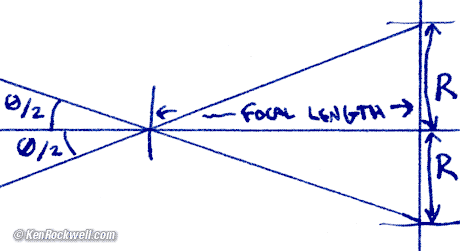
Angle = 2 * Arctan ( (Image Dimension/2) / Focal Length )
Ø = 2 * Arctan r/f
July 2007
Introduction
Angle-of-view is the breadth of a subject as seen by a camera system. It usually is stated for the diagonal of the image, and sometimes the vertical and horizontal.
A large angle shows a lot of things very small, and a small angle shows fewer things, but bigger.
It's a common camera and lens specification.
History
If you know your lens' focal length and an image dimension, high school trigonometry all you need is to calculate the angle of view.
You need to calculate the arc tangent to get your answer as an angle. I've been doing this since I was 11 years old, using a slide rule.
I lusted after Texas Instruments' first exotic electronic slide rule calculators so I could calculate these more easily back in the 1970s.
Today
Today, any scientific calculator can do this for a few dollars.
Better, Google knows all. Google also works as a calculator, free. Simply type your equation into the search box, and out pops your answer.
Here's the formula in Google format:
2 * arctan ([half dimension of image]/[focal length]) in degrees
The "in degrees" part is important, otherwise you'll get the answer in Radians!
Here are the values for some popular formats, in millimeters:
Diagonal, mm |
Vertical, mm |
Horizontal, mm |
|
26.7 |
14.8 |
22.2 |
|
28.4 |
15.6 |
23.7 |
|
34.5 |
19.1 |
28.7 |
|
FX and 35mm |
43.3 |
24 |
36 |
6x6 cm |
79 |
56 |
56 |
6x7 cm |
89.6 |
56 |
70 |
4x5" |
153.0 |
95 |
120 |
And here are one half of each of these values, which are the numbers to use typing into Google:
Half Diagonal |
Half Vertical |
Half Horizontal |
|
13.3 |
7.4 |
11.1 |
|
14.2 |
7.8 |
11.8 |
|
17.2 |
9.6 |
14.4 |
|
FX and 35mm |
21.6 |
12 |
18 |
6x6 cm |
39.6 |
28 |
28 |
6x7 cm |
44.8 |
28 |
35 |
4x5" |
76.5 |
47.5 |
60 |
Compact Cameras
Compact cameras' sensors oddly are specified with terms stolen from tube-type video cameras of the 1930s through 1970s.
A number like 2/3" referred to the diameter of the vacuum-tube imaging device, like an Image Orthicon or Vidicon, on the face of which would be a smaller active image area.
The diagonal of the active image area is usually 0.625 - 0.67x the nominal diameter of the tube (Burle, table 11-1).
Since I've worked in television engineering for decades, I get quite a chuckle that this is still with us decades after video tubes have fallen out of mainstream.
The active image area on a compact camera is much smaller than you would compute if you erroneously thought that a 1/1.8" nominal CCD had an active image diagonal that big (1/1.8" is 0.56" or 14mm.) The figures below are much closer to correct.
Diagonal |
Vertical |
Horizontal |
|
1/2.5" |
6.75 |
4.05 |
5.4 |
1/1.8" |
9.37 |
5.62 |
7.5 |
Half Diagonal |
Half Vertical |
Half Horizontal |
|
1/2.5" |
3.37 |
2.02 |
2.7 |
1/1.8" |
4.69 |
2.81 |
3.75 |
Examples
Most people refer to the diagonal angle of view, so I'll show these examples using diagonals. To calculate horizontal or vertical angles, use those dimensions instead.
18mm on DX
To calculate the diagonal angle of view of an 18mm lens on a Nikon DX digital camera, enter this into Google (copy and paste this line to see for yourself, or click the links):
2 * arctan (14.2/18) in degrees see example
Remember, without "in degrees," you get your answer in Radians.
14mm lens on full frame:
2 * arctan (21.6/14) in degrees see example
For a 210mm lens on 4x5:"
2 * arctan (76.5/210) in degrees see example
For a 2,000mm lens on Canon 1.6x:
2 * arctan (13.3/2000) in degrees see example
For a 5.8mm lens on a 1/2.5" Canon SD850 compact camera:
2 * arctan (3.37/5.8) in degrees see example
Units
Use the same unit for each measurement, millimeters, inches or any other unit, and everything is fine so long as you don't mix two units.
If you want to use different units, no problem, but you will have to name them, for instance, to calculate the angle of view of a 4-3/4" lens on 4x5" film, use
2 * arctan (76.5mm / 4 3/4 inches) in degrees
Spell out inches, since Google will interpret a """ mark as a quotation.
When using fractions, use a blank space, since a dash will be interpreted as subtraction.
Close Focus
This formula presumes images at infinity. Things become less predicable at closer distances.
Traditional lenses extend from your camera as they focus more closely, so they see a slightly narrower angle. No big deal, but if you worry about this, you know how to work the focus equation backwards to compute the slight extension of the lens.
I'm too lazy to calculate this for you folks, and even if I was, modern internally-focused lenses change their focal lengths as they focus. Therefore these formulæ no longer apply well enough to worry about small differences at close distances. The net effect of internal focusing is often to retain the same angle of view during closeups!
Internal focusing can confuse people, for instance, the Nikon 18-200mm lens reduces its effective focal length when focused closely at 200mm. At infinity it is 200mm, but as it focuses more closely it reduces its focal length, actually slightly increasing its angle of view! A traditional lens reduces its angle of view at closer distances.
Accuracy
Lens' true focal lengths are often up to 5% different than marked.
Along with barrel and pincushion distortion, the results from these calculated predictions will never be perfect. That's why I've always giggled at camera makers who present this data calculated to minutes of angle, since the size of the slide mount clear aperture or digital sensor varies from model to model, even if the lens is perfect.
Fisheyes
This formula presumes lenses without distortion. These calculations don't apply to fisheye lenses.
Different fisheyes use different projections, so different formulæ apply to different fisheye lenses.
If you know, let me know the projections of the 10.5mm Nikon and 15mm Canon fisheyes and the math for them and I'll add it.
Help me help you top
I support my growing family through this website, as crazy as it might seem.
The biggest help is when you use any of these links to Adorama, Amazon, eBay, B&H, Ritz, Calumet, J&R and ScanCafe when you get anything, regardless of the country in which you live. It costs you nothing, and is this site's, and thus my family's, biggest source of support. These places have the best prices and service, which is why I've used them since before this website existed. I recommend them all personally.
If you find this page as helpful as a book you might have had to buy or a workshop you may have had to take, feel free to help me continue helping everyone.
If you've gotten your gear through one of my links or helped otherwise, you're family. It's great people like you who allow me to keep adding to this site full-time. Thanks!
If you haven't helped yet, please do, and consider helping me with a gift of $5.00.
As this page is copyrighted and formally registered, it is unlawful to make copies, especially in the form of printouts for personal use. If you wish to make a printout for personal use, you are granted one-time permission only if you PayPal me $5.00 per printout or part thereof. Thank you!
Thanks for reading!
Mr. & Mrs. Ken Rockwell, Ryan and Katie.
Home Donate New Search Gallery Reviews How-To Books Links Workshops About Contact



